为了帮助大家能够提升计算速度,今天小编为大家带来一种可以快速计算的方法——特征数字法。所谓特征数字法,就是将计算过程中数据的前若干位有效数字视为特征数字,再转化为分数的计算方法,通常用于乘除运算中,用以简便计算。为了加深大家的理解,我们来看几个例题。
例1、12345×12.5%=( )
A.1305
B.1453
C.1543
D.1672
【解析】 选择最为接近的C选项。
选择最为接近的C选项。
通过例1我们发现,如果按照原式中的乘法按部就班地进行计算,过程较为复杂,会浪费掉不必要的时间,当我们灵活地将百分数转化为对应的分数后,可以极大地减少运算量,节约时间。接下来我们再来看一道例题。
例2、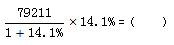
A.9800
B.10100
C.11200
D.12400
【解析】将原式中的百分数进行转化,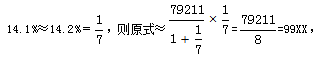 选择略小的A选项。
选择略小的A选项。
大家仔细观察第二个例题,我们选择了略小的A选项,这里就涉及了放缩。当选项比较接近的时候,我们就要注意特征数字与原百分数的大小关系,尤其在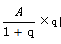 的列式形式中,当q在转为特征数字中变大时,整体计算出的数据偏大,要选择与之接近较小的选项。当q变小时,整体计算出的数据偏小,要选择与之接近较大的选项。
的列式形式中,当q在转为特征数字中变大时,整体计算出的数据偏大,要选择与之接近较小的选项。当q变小时,整体计算出的数据偏小,要选择与之接近较大的选项。
例3、54321×16731=( )
A.7.65亿
B.9.09亿
C.11.42亿
D.13.57亿
【解析】选项数量级相同,只需观察有效数字,无需考虑数位及小数点的影响。题干中16731的前三位有效数字为167,考虑利用特征数字法解题,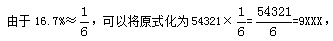 选择有效数字最为接近的B选项。
选择有效数字最为接近的B选项。
在例3中,我们发现虽然相乘的两个数字都是整数,但我们仍旧可以利用特征数字法将其转换分数进行求解。所以大家要开拓思维,不局限于“百化分”的这一种情况,而是聚焦于数字的“特征”,灵活利用,才能在实际做题中更快地解出答案。
下面是小编为大家整理的常见百分数与分数之间的转换:
通过以上三道题目,相信大家对特征数字快速计算的方法有了一定的了解,希望各位同学在复习过程中多加练习,加以应用。


 天津公务员行测难点及技巧总结
天津公务员行测难点及技巧总结  行测资料分析例题讲解
行测资料分析例题讲解 选择最为接近的C选项。
选择最为接近的C选项。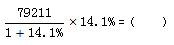
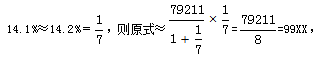 选择略小的A选项。
选择略小的A选项。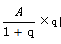 的列式形式中,当q在转为特征数字中变大时,整体计算出的数据偏大,要选择与之接近较小的选项。当q变小时,整体计算出的数据偏小,要选择与之接近较大的选项。
的列式形式中,当q在转为特征数字中变大时,整体计算出的数据偏大,要选择与之接近较小的选项。当q变小时,整体计算出的数据偏小,要选择与之接近较大的选项。 选择有效数字最为接近的B选项。
选择有效数字最为接近的B选项。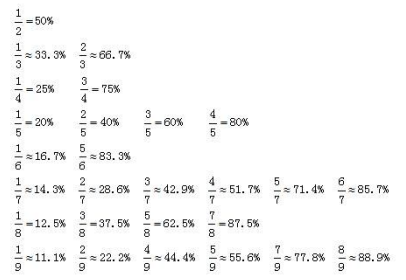
 更多天津公务员考试行测技巧与方法扫码获取
更多天津公务员考试行测技巧与方法扫码获取

 行测技巧储备不够?扫码回复“咨询老师”
行测技巧储备不够?扫码回复“咨询老师”


