特殊角度法就是根据我们比较熟悉的一些角度的大小，找到某个部分对应到扇形的角度范围，大致能判断出某个部分的角度占比，再对比选项中图形特点确定答案。具体而言就是，如果一个部分占整体比重为½，扇形角度就是180°；比重为⅓，扇形角度就是120°；比重为⅔，扇形角度就是240°；比重为¼，扇形角度就是90°；比重为¾，扇形角度就是270°等等。
例1、材料：调查结果显示，66%的网民对本市的市场管理满意，较满意的占28%，6%的网民认为不满意。
问题：下列哪项反映了此次调查中网民对本市的市场管理的满意程度？
【解析】答案选D。占比最大的满意，占到66%，超过整体的50%，那么最大部分的扇形角度就应该大于180°，排除B、C，比重第二大的是28%，较为接近且略大于扇形角度近似为90°，只有D选项符合。
二、角度倍数与数据倍数一致
当两个数字间有明显倍数关系的时候，例如A是B的两倍，A的角度就是B的两倍，再查找具有这个特点的选项。
例2、材料：2015年，四川省生产总值为30103.1亿元，重庆市生产总值为15719.72亿元，云南省省生产总值为13717.88亿元，贵州省生产总值为10502.56亿元，西藏省生产总值为1026.39亿元。
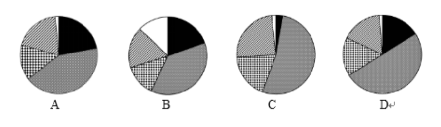
问题：能够正确描述2015年西南地区五省(区，市)生产总值(五省总产值为71069.65亿元)占比的统计图是：
【解析】答案选A。四川省的生产总值最大为30103.1亿元，小于五省总产值71069.65亿元的一半约为35534亿元，因此占比最大的四川省比重小于50%，扇形的圆心角应小于180°，排除C和D选项，余下地区西藏1026.39亿元最小，次小的是贵州地区10502.56亿元，贵州大约是西藏的10倍，因此圆心角也是10倍。而B选项中最小的扇形与其他部分相差不多，不符合，所以选A。
从角度特征，部分之间倍数关系特征入手，对于解决选项为图形类资料分析题目来说百试不爽，希望同学们不被这种题型吓到，抓住比例与角度的关系，通过训练，实现运用自如，从而在考场上冷静应对，资料分析还有很多巧妙的方法，让看似复杂的问题可以迎刃而解，需要同学们加强学习，善于总结。
2023年天津公务员考试行测资料分析之“饼图”占比问题
例题讲解，做好笔记
