例1、有10个相同的苹果,分给3个小朋友,每个小朋友至少一个,问共有多少种分法?
A.45
B.36
C.120
D.42
【解析】B。根据题意,10个相同的苹果分给3个小朋友,也就是把苹果分成3堆。那么将10个苹果排开,只需要往苹果与苹果的空隙之间插入2块板,就可以分为3堆。因为每个小朋友至少一个,所以只能在10个苹果中间的9个空隙中插入2块板,因为空与空之间是相同的,改变顺序对结果没影响,用组合数,答案为36。所以答案选择B。
上述例题就是一个简单的“隔板法解决同素分堆”的题目,就是将相同的东西分给几个人,我们在东西的中间空隙用板子隔开进行分堆即可,接下来一起来总结一下可以用隔板法解题的题型特征以及解题公式。
题型特征:把n个相同元素分给m个不同的对象,每个对象至少1个元素,问有多少种不同分法的问题。1.所要分配的元素必须完全相同(例如10个相同的苹果)。2.每个对象至少分到1个(比如每个小朋友至少一个)。
解题公式:方法数共有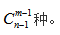
了解题型特征以及公式后,那我们来看看怎么来灵活地运用“隔板法”呢?
例2、把10个相同的苹果分给3个小朋友,每个小朋友至少2个,问共有几种分法?
A.15
B.21
C.20
D.42
【解析】A。根据题目,“10个相同的苹果”说明相同元素,“分给3个小朋友”说明要分成3堆,但是题目中是“每个小朋友至少2个”,与题型特征中“每个对象至少1个”不符,不能直接使用“隔板法”,所以我们要先把“至少2个”变为“至少1个”。如果先给每个小朋友发1个苹果,现在苹果还剩10-3=7个,7个相同分发给3个小朋友,每个小朋友至少1个,直接使用公式,答案为15,选择A。
相信大家通过上述题目的讲解,能对“隔板法”有一定的了解。小编建议大家在备考期间需多多练习,真正做到熟练掌握这类问题,希望对于大家的备考能有所帮助。


 天津公务员考试行测数量关系,巧解同素分堆问题
天津公务员考试行测数量关系,巧解同素分堆问题 例题讲解,做好笔记
例题讲解,做好笔记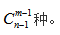
 更多行测技巧与方法扫码获取
更多行测技巧与方法扫码获取

 常识储备不够?扫码回复“咨询老师”
常识储备不够?扫码回复“咨询老师”

