因此,小编建议大家:首先大家要明确数量关系这一部分的重要性——它是拉高总分、拉高行测整体正确率的重要板块;其次,数量关系也有简单和中等难度的题目,并不是所有题目都是难题。针对数量关系部分,我们其实可以挑选性价比高的题目去做。
所以,在复习数量关系时,首先要能夯实基础概念、掌握基础的“方程法”,其次再去掌握一些快速解题的技巧和能力、提高准确率和做题速度。下面,让我们以几道题目为例,从“方程法”出发,再到“新方法”的应用,来体验一些不一样的解法吧!
【例1】林先生要将从故乡带回的一包泥土分成小包装送给占其朋友总数30%的老年朋友。在分包过程中发现,如果每包200克,则少500克;如果每包150克,则多250克。那么,林先生的朋友共有多少人?
A.15
B.30
C.50
D.100
【答案】C。解析:
方法一(方程法):设林先生分了x包泥土给老年朋友,因为泥土的总量是不变的,所以可以根据两种分配方案下泥土总量不变列方程,200x-500=150x+250,解得x=15。因老年朋友占朋友总数的30%,因此林先生共有15÷30%=50位朋友。选择C项。
方法二(盈亏思想):根据题目,在前后两种分配方案对比中,泥土的总量始终是不变量,若每包200克则缺500克,若每包150克则多250克。因此如果想让每包在分得150克的基础上,每包都增加50克(增加到每包200克),则里外里相当于还需要250+500=750克。则分的小包装、即老年朋友数为750/50=15。因老年朋友占朋友总数的30%,因此林先生共有15÷30%=50位朋友。选择C项。
【要点提示】当题目涉及类似“两种方案对比中具有不变量”的问题时,我们既可以用“方程法”解题,又可以借助”盈亏思想”,简单口算达到快速解题的目的。
【例2】将300克浓度95%的酒精与若干浓度60%的酒精,混合成浓度75%的酒精,需要浓度60%的酒精多少克?
A.225
B.240
C.380
D.400
【答案】D。解析:
方法一(方程法):设需要浓度60%的酒精x克,根据混合前后溶质质量不变,则有75%×(300+x)=95%×300+60%x,解方程得x=400。选择D项。
方法二(十字交叉法):因为题目涉及到两种浓度的溶液混合,浓度=溶质/溶液,本质上是比值的混合问题,因此根据十字交叉法有:
则有15%/20%=300/x,解得x=400。选择D项。
【要点提示】当涉及到类似A/B比值的混合问题时,我们不仅可以用“方程法”解题,还可以借助“十字交叉法”帮助我们减少列式书写的步骤,从而达到快速解题的目的。
以上题目为大家浅浅展示了在方程法以外的一些解题方法。大家在夯实基础之后,可以多开拓思维,在实战中进一步提升能力。


 更多行测技巧与方法扫码获取
更多行测技巧与方法扫码获取
 天津公务员行测数量关系“快解法”,白捡知识!
天津公务员行测数量关系“快解法”,白捡知识! 例题讲解,做好笔记
例题讲解,做好笔记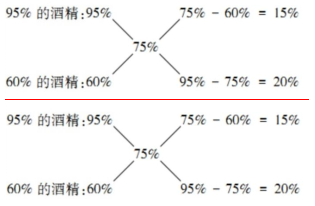
 常识储备不够?扫码回复“咨询老师”
常识储备不够?扫码回复“咨询老师”

