研究这几年的省考真题,我们会发现考试数量关系题型越加多元化,不在局限于几种常规题型了,专家建议大家在备考中就需要关注一些新题型,比如货物集中问题。
(1)什么是货物集中问题?
定义:货物集中问题即集中统筹问题,是指在将货物集中的同时,使得货物的运费最省。
(2)货物集中问题遵循的原则:
即在非闭合路径上(如直线)有多个“点”,点上有一定重量的货物,每个点之间由一定的路径连接,把货物集中到一点上最优的方式。遵循原则:确定一点,判断该点两端货物的重量,把轻的一端向重的一端集中。注意:在决定货物往何处集中时,起决定作用的是货物的重量,至于距离仅仅是为了计算运费。
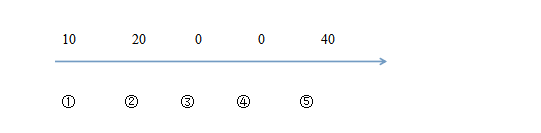
例题1、在一条公路上每隔100公里有一个仓库,共有5个仓库,一号仓库存有10吨货物,二号仓库存有20吨货物,五号仓库存有40吨货物,其余两个仓库是空的。现在要把所有的货物集中存放在一个仓库里,如果每吨货物运输1公里需要0.5元运输费,则最少需要多少运费?
A.4500元 B.5000元 C.5500元 D.6000元
【解析】B。方法一:如果都运到一号仓库,需要运费(20×100+40×400)×0.5=9000元;
如果都运到二号仓库,需要运费(10×100+40×300)×0.5=6500元;
如果都运到三号仓库,需要运费(10×200+20×100+40×200)×0.5=6000元;
如果都运到四号仓库,需要运费(10×300+20×200+40×100)×0.5=5500 元;
如果都运到五号仓库,需要运费(10×400+20×300)×0.5=5000 元。
由以上可知,都运到五号仓库,需要运费最少,为 5000 元。
方法二:利用原则可知:本题四条“路”都具备“左边总重量轻于右边总重量”的条件,所以这些路上的流通方式都是从左到右,因此集中到五号仓库是最佳选择。即先把一号仓库 10 吨的货物移动到二号仓库那,这样二号仓库就相当于有了 30 吨货物,但仍然少于五号仓库的 40 吨货物,因此再把二号仓库 30 吨的货物移动到五号仓库。
确定是五号做仓库,那么直接算费用:10×400×0.5=2000,20×300×0.5=3000,合计5000元。相比较方案一,显然二方案会简单很多。
例题2、(18年江西省考真题-71)在一条公路上每隔10里有一个集散地,共有5个集散地,其中一号集散地有旅客10人,三号集散地有25人,五号集散地有45人,其余两个集散地没有人。如果把所有人集中到一个集散地,那么,所有旅客所走的总里数最少是:
A.1100 B.900 C.800 D.700
解析:采用支点比较法。把支点设在 ① ② 之间,支点左边是 10,支点右边是 70,
左边小于右边,支点继续往右移,设在② ③之间,此时支点左边是 10,支点右边是 70,左边小于右边,支点继续往右移,设在 ③④ 之间,此时支点左边是35,支点右边是 45,左边小于右边,支点继续往右移,设在 ④⑤ 之间,此时支点左边是 35,支点右边是 45,左边大于右边,此时支点左边的点 ⑤ 点即为所要求的点。所求费用:10×40+25×20=900选B。
需注意问题:1、必须适用于“非闭合”的路径问题中;
2、此问题的解决,与各条路径的长短没有关系;
3、实际操作中,我们应该从中间开始分析,这样可以更快得到答案
综上所述,货物集中问题只要找到了解题方法,都可以迎刃而解,各位考生在备考时,要特别注意审题,理好解题思路,找到最快速的解题方法,方能在考试时立于不败之地。